调整最小不平衡子树
什么是平衡二叉树?
平衡二叉树(Balanced Binary Tree),简称平衡树(AVL树)——树上任一结点的左子树和右子树的 高度之差不超过1。
结点的平衡因子=左子树高-右子树高。
什么是最小不平衡子树?
往一个平衡二叉树(本文中均指“平衡二叉排序树”)插入新的叶子节点,从插入点由下往上,依次遍历插入点的各个祖先节点,记录第一个遍历到的 平衡因子|平衡因子|≥2 (即不平衡)的祖先节点,以该节点为根节点的子树即为这棵树的最小不平衡子树。
根据插入节点在最小不平衡子树中的位置,可以将最小不平衡子树分为LL、RR、LR、RL这四类
在处理问题前,先将最小不平衡子树抽象、简化为以下部分中的几个:
- 最小不平衡子树的根节点A
- A的左子树AL(A-Left)
- A的右子树AR(A-Right’)
- A在插入点对应侧的子节点B
- B左子树BL(B-Left)
- B右子树BR(B-Right)
- 插入节点所在的子树Ins(Insert)
LL型与RR型
LL型
插入点在最小不平衡子树根节点A的左孩子B的左子树上(不一定要与B直接连接),即Left-Left,记为LL型
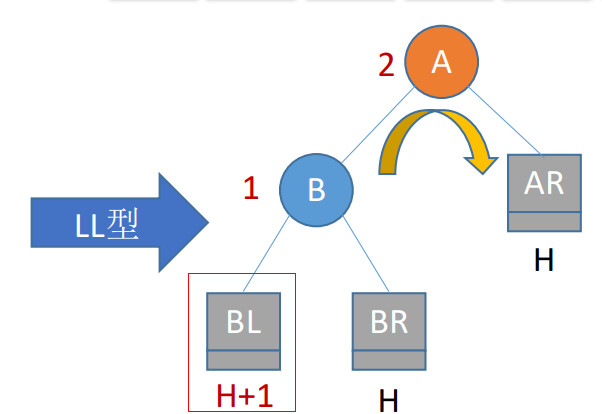
对于LL型,将最小不平衡子树简化为五个部分:
- 根节点A
- A的左孩子节点B
- A的右子树AR(A-Right)
- 插入点Ins(全称Inserted),此时同时也是B的左子树BL(B-Left)
- B的右子树BR
这里注意无论AL、AR、BL、BR、Ins下有多少个节点,也无论插入的元素在Ins的哪个位置,都抽象成以上几个部分,再处理问题
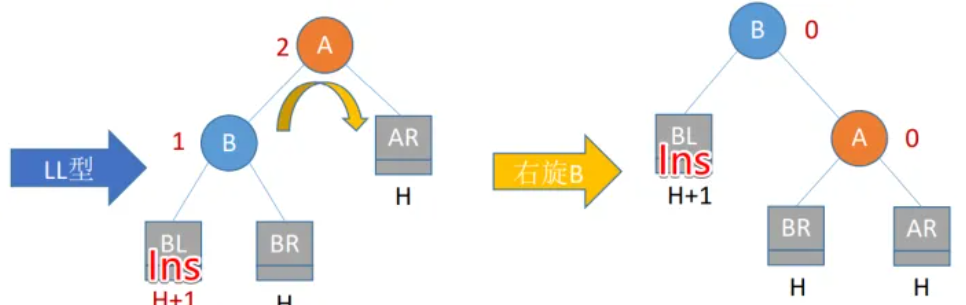
对于LL型,进行右旋,B取代A成为根节点,A当B的右孩子(对应右旋),A以两个除Ins之外的树为子树(注意两子树的相对左右顺序与旋转前一致),B以Ins树为左子树
RR型
插入点在最小不平衡子树根节点A的右孩子B的右子树上(不一定要与B直接连接),即Right-Right,记为RR型
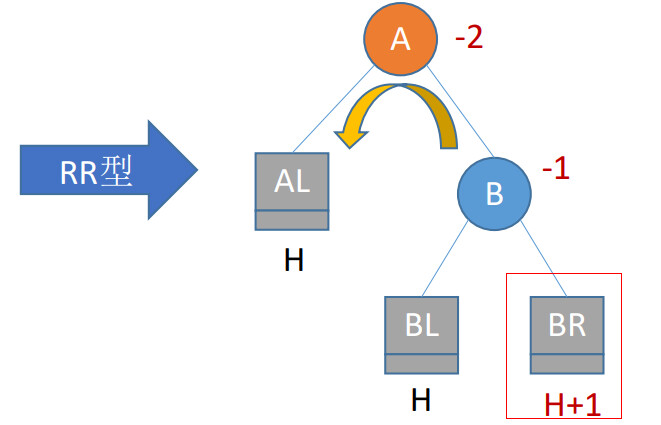
将RR型最小不平衡子树简化为五个部分:
- 根节点A
- A的右孩子节点B
- A的左子树AL
- 插入点Ins,此时同时也是B的右子树BR
- B的左子树BL
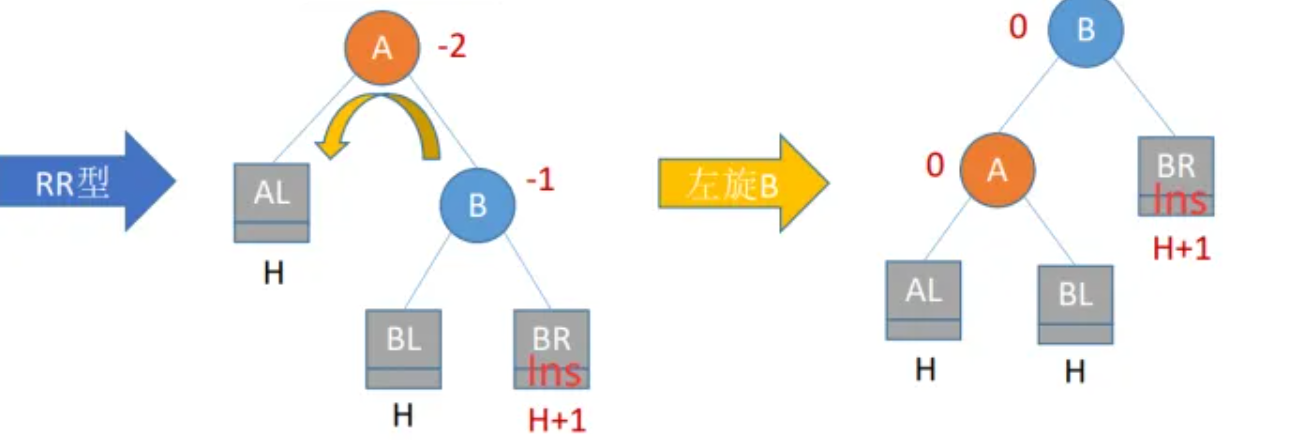
对于LL型,进行左旋,B取代A成为根节点,A当B的左孩子(对应左旋),A以两个除Ins之外的树为子树(相对左右顺序与旋转前一致),B以Ins树为右子树
LR型与RL型
LR型与RL型稍复杂,在简化与抽象时,较前面划分的几个part之外还增加了:
- 插入节点所在子树的父节点C
- C节点的左子树CL(C-Left)
- C节点的右子树CR(C-Right)
LL型与RR型只需要简化成五个部分,而LR型与RL型则需要简化成七个部分
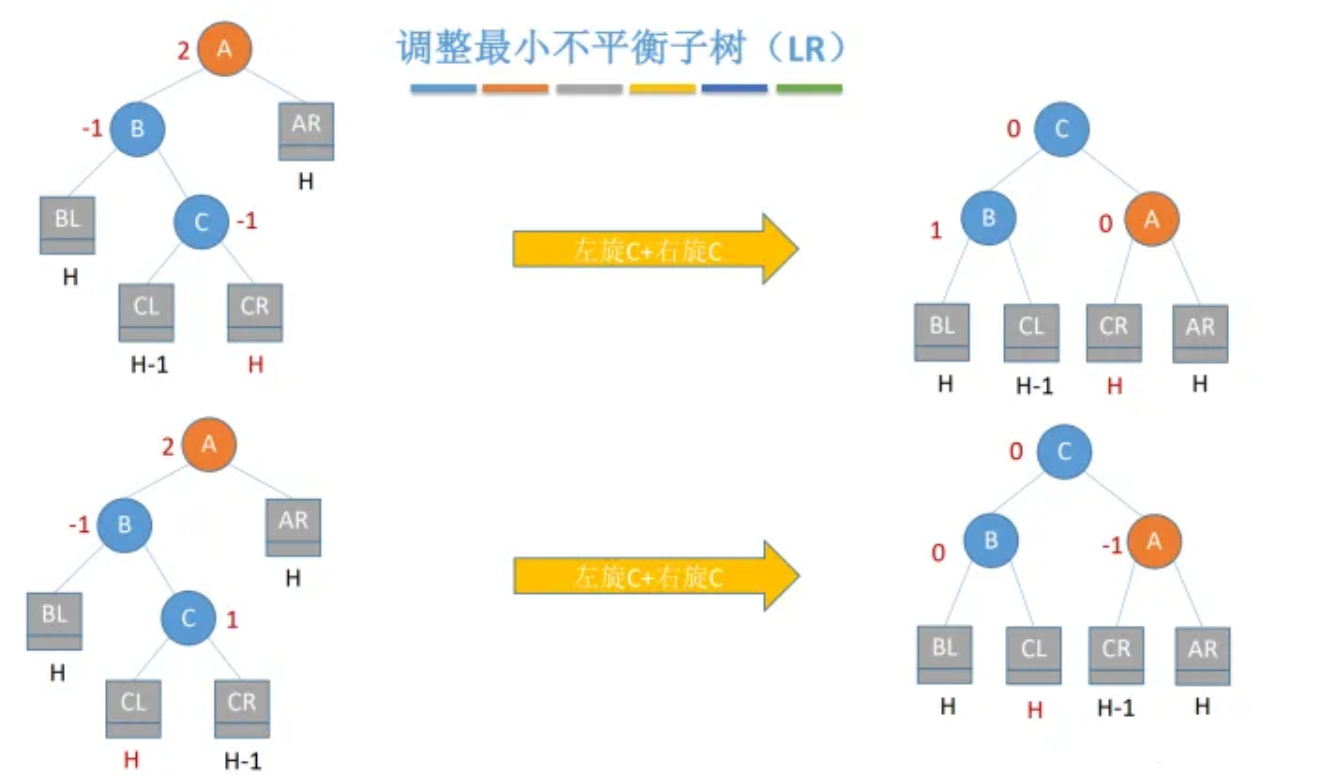
LR型
插入点在根节点A的左孩子B的右子树C上(不一定要与C直接连接),即Left-Right,记为LR型
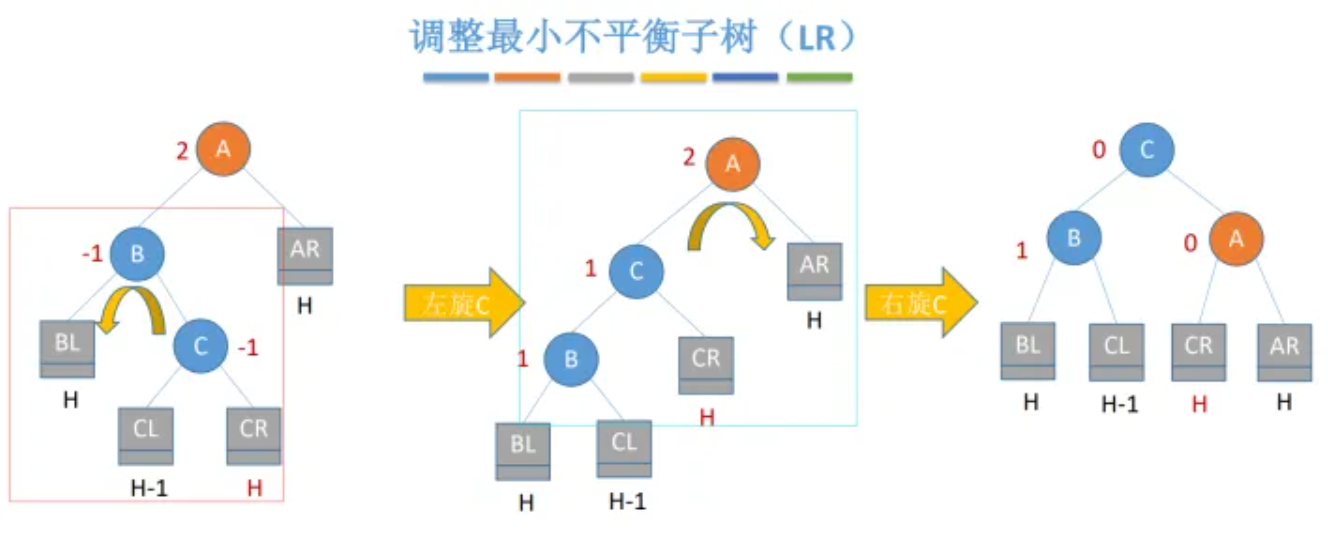
无论Ins是在C的左子树上还是右子树上,都先把第一步红框中的部分左旋(Left),C取代B的位置,以B为左孩子节点,以CR为右孩子,B将以BL为左子树、CL为右子树;
接着把第二步中蓝框的部分右旋(Right),C取代A的位置,依然以B为左孩子节点,以A为右孩子节点,A将以CR为左子树、AR为右子树;
RL型
插入点在根节点A的右孩子B的左子树C上(不一定要与C直接连接),即Right-Left,记为RL型
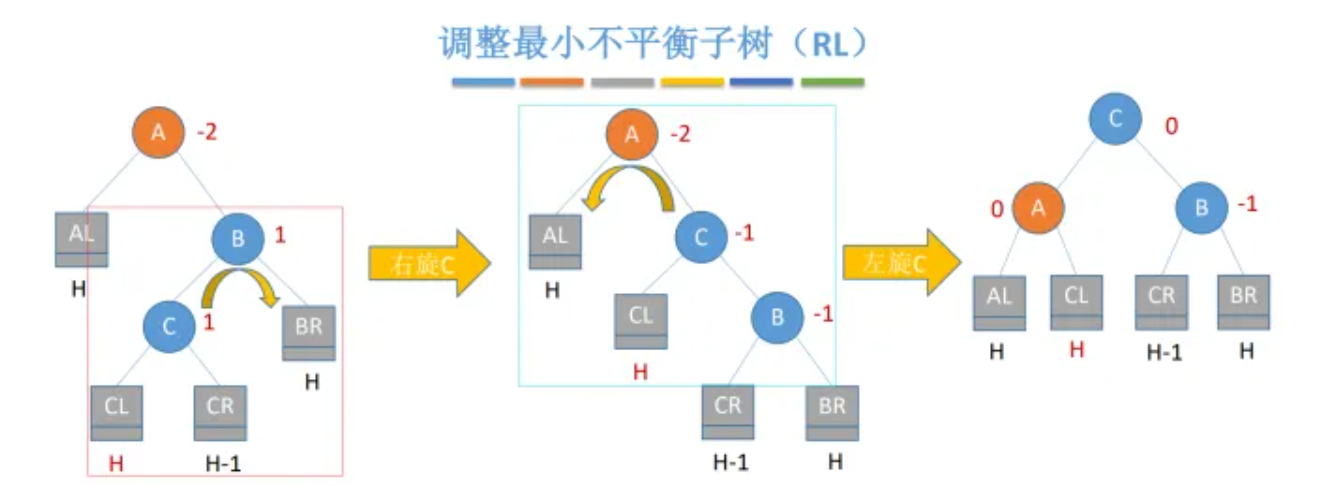
无论Ins是在C的左子树上还是右子树上,都先把第一步红框中的部分右旋(Right),C取代B的位置,以B为右孩子节点,以CL为左孩子,B将以BR为右子树、CR为左子树;
接着把第二步中蓝框的部分左旋(Left),C取代A的位置,依然以B为右孩子节点,以A为左孩子节点,A将以AL为左子树、CL为右子树;
验算小技巧
旋转后左右次序不变,调整前夹在两祖宗节点之间的子节点,在调整后依然要夹在两祖宗节点之间
参考资料
王道计算机考研数据结构篇